The Solution for Learning Mathematics is the Solution
Written by Jay Meadows, M.Ed, MAT, Exemplars CEO

The very first question I asked when I came to work for Exemplars was “does it work?” Do performance tasks actually improve student learning? We hired a former teacher turned educational researcher, David Adler of Recontext, to help us investigate this question. David worked to evaluate the 130+ schools in New York City who had been using our performance tasks for at least three years to determine if there was any noticeable improvement in their students' proficiency on the state exams. David’s research provided us with the following data reflected in the graph below.
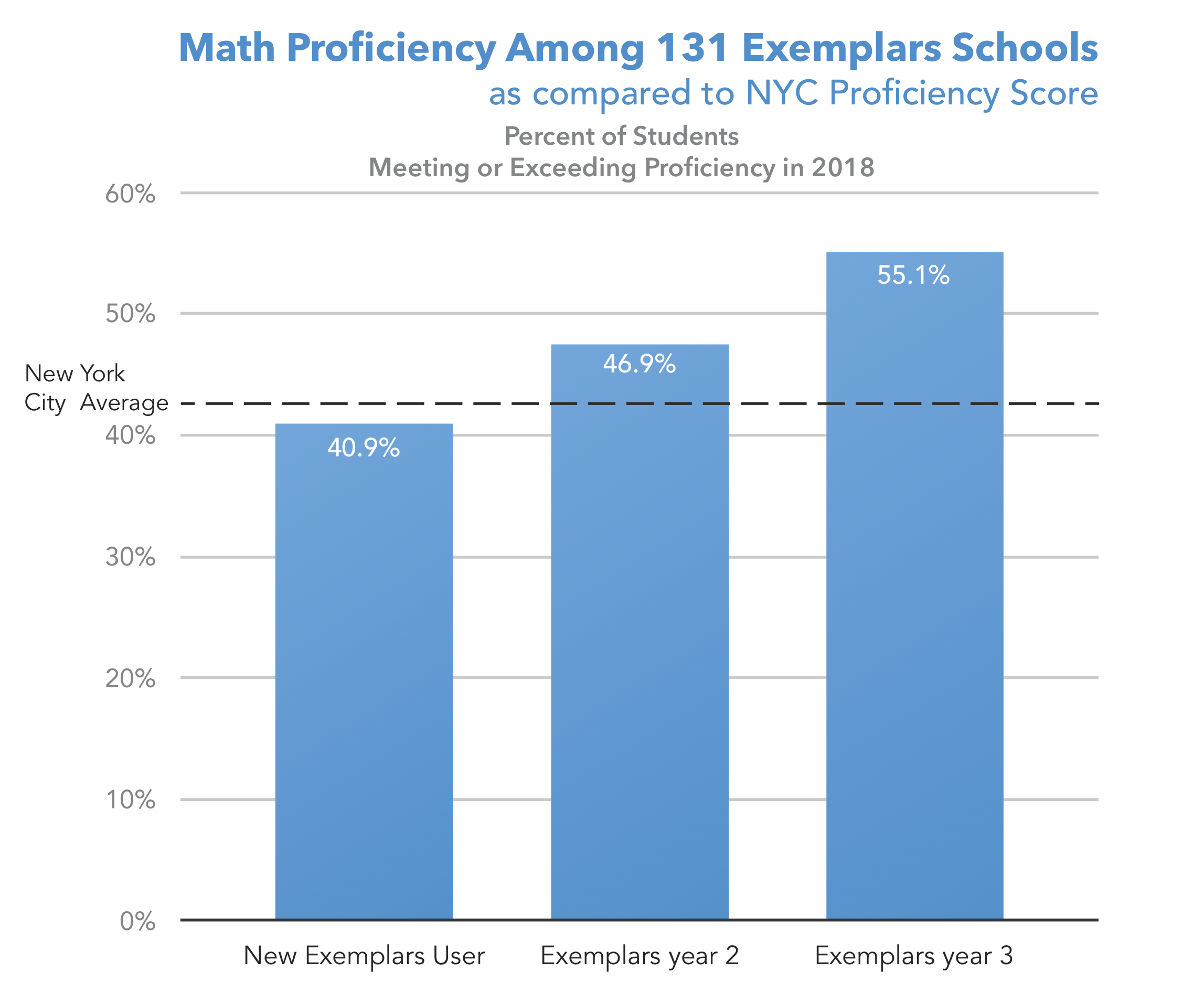
Results from 131 NYC Schools
At almost the exact same time, Edutopia published an article that investigated how a school in the Bronx, NYC managed to transform from an extremely low-performing school into one of the highest-performing schools in the entire city. Their conclusion? The constant use of Exemplars performance tasks was a “game-changer” for students’ math performance.
The next question became why? And how? How could performance tasks demonstrate such a powerful impact on student learning?
The search for the answer took me deep into the research of effective education and eventually brain research. The summary? The expectations and opportunities built within performance tasks consolidates the highest level of educational pedagogy.
What follows is a brief summary of how performance tasks activate the brain and how performance tasks are effective in helping students learn mathematics.
Brain-Based Learning
Within their highly acclaimed book Brain-Based Learning (2020), researchers Eric Jensen and Liesl McConchie unpack years of study to explain for educators how the information being discovered within cognitive neuroscience and educational research can be understood and utilized within the classroom. An important element of the book focuses on “Better Classroom Learning.” The summary of the research focuses on three stages of classroom learning: Readiness, Coherent Construction, and Consolidation.
The power of performance tasks is defined throughout these three stages. Let's explore one specific element within each phase.
Readiness
The first element in learning is readiness—the brain needs to want to learn. More specifically, the brain needs to be “primed” to want to learn. Until the student decides that the information they are about to experience is going to improve their life, the brain has no need to expend the incredible time and energy required to learn it. This is about relevancy: If the learning is not relevant to the student, the brain will not learn it.
As an educator, how can you engage your students to help them want to learn? You have to find ways to make mathematics relevant. To do this we can start by answering the age-old classroom question from our students: “When am I ever going to use this?” If we help students answer this question, suddenly the brain decides to turn on. The brain literally asks “What’s in it for me?” (McREL) As educators, it is our responsibility to answer this question.
Performance tasks can help us answer this question. The real-world context of a well-designed task can demonstrate for students that the math concepts they are learning in the classroom actually do have value. A well-designed performance task articulates a real-world situation in which mathematics becomes a powerful tool to solve a real problem. We have to provide students with problems worth solving.
Coherent Construction

The next stage of learning includes the “coherent construction” of new information. A vital element of this includes “multisensory instruction.” The brain stores different types of information in different regions of the brain. Vocabulary and language are stored in the temporal region of the brain, directly around the ears. This makes sense right? Language is stored right above the ears.
Visual information is stored and processed in the occipital lobe of the brain. This region is positioned in the back of the brain. (Curious though that this is the farthest region from the eyes.)
The region which is designed to bring information from various parts of the brain together and process higher-level cognitive activities is the prefrontal cortex, found near the front of the brain. Here, all of the various elements of thinking come to be put together and to construct the big picture. This is also the region where we manipulate what we know, our prior knowledge, into new knowledge. Motion and physical activity in the hands happens in the motor cortex, located between the parietal lobe and the prefrontal cortex.
Interestingly, mathematical thinking seems to happen in various parts of the brain. Depending on the type of mathematics the mind is working on determines which areas of the brain seem to activate. Mathematical activity might occur in the prefrontal cortex, the parietal lobe which is positioned near the top of the brain, along with the temporal lobe and the occipital lobe. Each region may activate for different kinds of mathematical thinking, depending on the math task. Often multiple regions of the brain will activate simultaneously while engaging in a complex math task.
To help students learn mathematics, “teachers should attempt to target multiple sensory cortices within each learning experience” (Jensen and McConchie, 2020, p. 175). Translation: we need to create opportunities for our students to engage each region of the brain during a learning experience. How do we ask students to engage the language region, the visual region, the math regions, the physical region and bring it all together? By using a well-designed performance task and by having students write a well-written solution.
This solution is the student’s attempt to justify their answer. A performance task will ask students to use models and representations to manipulate and visualize the math strategy the students want to use to solve the problem. This activates the occipital region. A solution will ask a student to explain their reasoning for how and why they solved the problem the way they did. A solution invites a student to utilize their bank of mathematical vocabulary as part of their explanation. Thus the temporal region is now activated. A student will also need to show any calculations they used to solve the problem. Now the parietal, temporal, occipital and prefrontal regions are all activated.
So why do solutions improve student proficiency on state tests? My working theory: “The neurons that fire together stay together.” My theory is that as a student writes their solution by hand, each of the regions in their brain is activated. The words in the temporal region connect with the visuals in the occipital region, which connect with the parietal region, which all connect with the prefrontal cortex. Visuals, words, calculations all connect. And the regions are all activated for an extended duration as the student writes their solution. Regions are connected. Visuals, words, calculations all connect. At Exemplars, we call this “performing” mathematics.
Consolidation

The final stage of the learning process is consolidation. This is the brain activity where we make sense of what we learned, we make meaning of the experience, and we encode the new learning into our long-term memory. When we think about consolidation, there are two important moments in the process. First is consolidation of the information into the appropriate regions of the brain. The second is the “reconstructive process” of putting the information back together when we want to use it.
“Spaced learning” involves asking students to re-engage with information they have learned over time. How we put together various mathematical concepts we have learned in the past back together is exactly what performance tasks do. A well-written performance task will create a real-world situation that will require multiple mathematical calculations and strategies to be utilized to arrive at a correct, reasonable answer. A student practices recalling from their prior knowledge the right tool for a specific situation. Within a real-world context, a student has to recall how that algorithm or formula or math process actually works. So now a student has not only practiced remembering an important skill, but their mind is recognizing the real-world context in which it is useful. “What’s in it for me” has been addressed while remembering has been practiced.
This leads us to the final element of consolidation:“relevant transfer.” Jensen and McConchie suggest that few elements of learning are as important to learning something as the concept of relevant transfer. This idea focuses on the “why” students are engaging in learning something new. This stage also invites students and teachers to consider how a new activity or math skill connects with ideas they have learned in the past. When students can see for themselves how the concepts within mathematics all fit together and build on each other, suddenly math transforms from a random set of procedures into a powerful toolkit of strategies to solve any problem put in front of them.
Summary
Cognitive neuroscience has been working to help educators understand how the brain learns and what conditions we can introduce in our classrooms that will improve the effectiveness of learning. What is amazing is that performance tasks have been synthesizing the most salient elements of these new findings within cognitive neuroscience for over 30 years.
Asking students to solve an authentic, real-world problem, utilizing their internal toolkit of strategies and prior knowledge to reach a reasonable answer and then work to explain their thinking in a coherent justification utilizing representation, language and calculations to solve one mathematical task can activate the highest level of mathematical thinking and learning.
Jensen, E., and McConchie, L. (2020). Brain-Based Learning: Teaching the Way Students Really Learn (3rd ed). Corwin.

Fifth Grade Student Solution Exemplar

