Written by: Jay Meadows, Exemplars, CEO

I know, I know—“fail” is a very strong word. Yet when the results came in, only 36% of 4th graders and 26% of 8th graders across the United States performed at or above the proficient level on the National Assessment of Educational Progress (NAEP) mathematics assessment. Quickly, the question, “Why?” was being asked across the country. 

The NAEP, also known as The Nation’s Report Card, calls itself, “the assessment [that] measures students' knowledge and skills in mathematics and their ability to solve problems in mathematical and real-world contexts.”   

So why did the vast majority of American students struggle on the NAEP? In order to find an answer, I decided to take the NAEP tests myself. Having written numerous mathematics assessment questions over the years, I was curious: What exactly were the NAEP’s questions asking our students to do?

By the time I completed the fourth question on the 8th grade assessment, I began to identify some of the specific challenges students were encountering on the NAEP assessment: 

First, the questions are HARD! They’re not impossible, nor are they written to be confusing; but the questions do require students to demonstrate a strong flexibility with mathematics. 

Many of the questions on the NAEP have multiple correct answers, and students are expected to find all of them. These types of questions are likely to be particularly challenging for students who have been educated in classrooms where calculations and the utilization of algorithms has been the focus. In such classrooms, there is usually only one correct answer. Use an algorithm correctly, you will get the right answer. Make a mistake, and you’re told you’re wrong.

NAEP Sample Questions

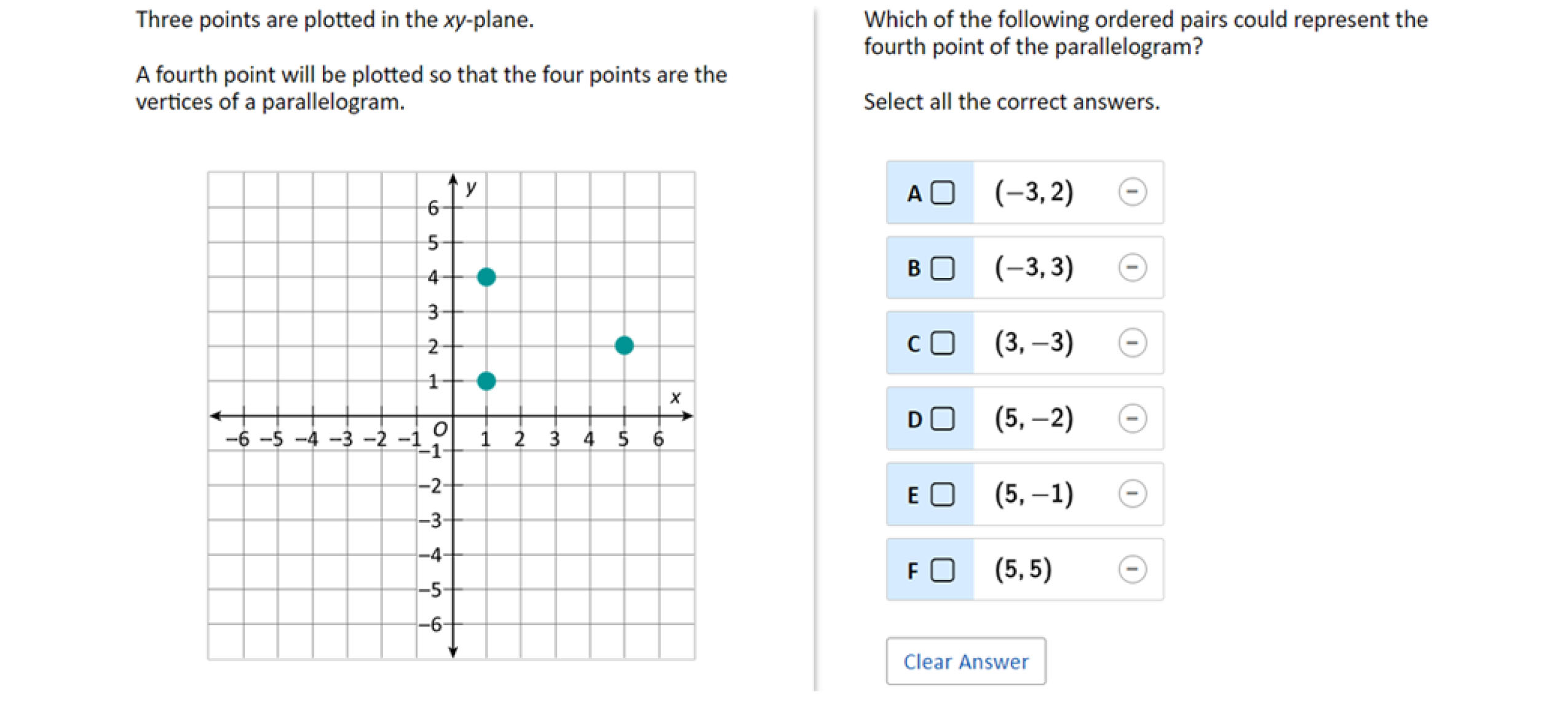
Source: The Nation's Report Card

Second, the questions involve significant reading. Grade-level mathematical vocabulary is embedded unapologetically throughout the questions. If students have not worked diligently in their classrooms to develop a working understanding of mathematical vocabulary, these questions will be highly difficult to decipher. Students must also define for themselves what problem they need to solve.  

Next, the NAEP questions generally provide no scaffolding. The expectation of the question is presented in as few words as possible, and students must define for themselves the multiple steps that will be needed to arrive at a final answer. Students must recall the required mathematical concepts they need to utilize to solve the problem. With multiple undefined steps and multiple mathematical concepts embedded within a task, students must have strong skills with application and flexibility with their mathematical toolkits.  

NAEP Sample Questions

Source: The Nation's Report Card

Often, information required to reach the final answer is embedded within various places on the page. Frequently, information must be extracted from graphs and tables, then combined with additional information shared within the original question.

Many questions demand significant flexibility in mathematical thinking. The NAEP questions do offer a few questions which expect a straightforward utilization of an algorithm, but the majority of the questions require flexible application of mathematics in unfamiliar situations. Expectations for strong critical thinking are baked into most of the questions.

Representations are also utilized throughout the assessment. Students must know how to utilize and manipulate number lines, graphs, tables, diagrams, and geometric shapes. It’s clear that the NAEP assesses conceptual understanding more frequently than procedural fluency. Conceptual understanding develops in classrooms that spend significant time allowing students to explore mathematics in a more “hands-on” way with tools, manipulatives and representations that build deeper understanding of mathematical concepts.

NAEP Sample Questions

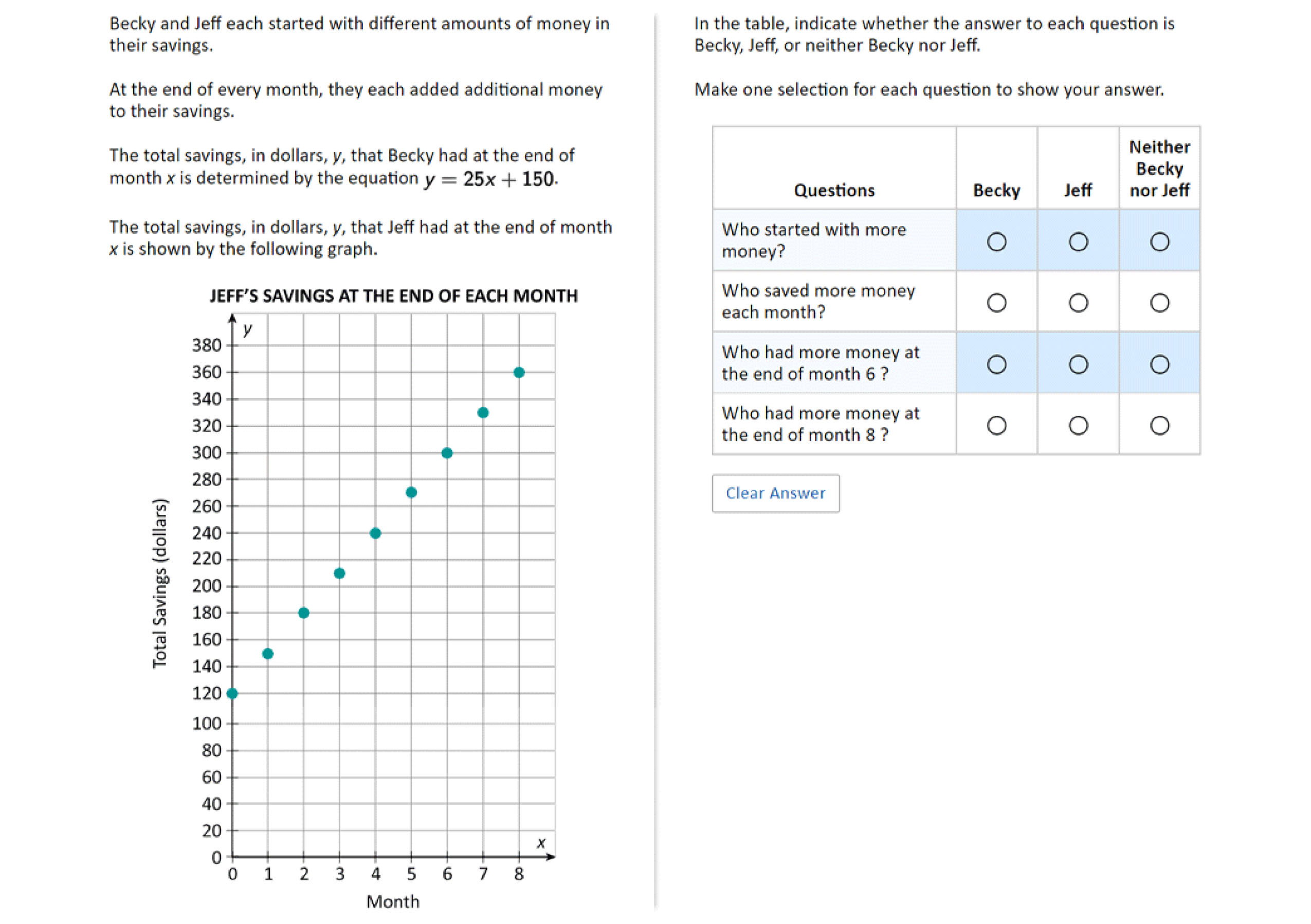
Source: The Nation's Report Card

Overall Thoughts

So, what do I think of the NAEP assessment questions? I like them. The NAEP defines itself as an assessment that measures students’, “ability to solve problems in mathematical and real-world contexts” and I wholeheartedly support this goal. 

With the NAEP’s stated goal in mind, should we assess and thereby know whether or not students can transfer the concepts and algorithms they are learning in their math classrooms in order to address the complex challenges and requirements of the real world? Yes, if we want to raise a generation of students prepared to solve the pressing challenges of the 21st century, I believe we should.  

Times have changed. The days of spending the bulk of our time in math classrooms training students to be highly efficient and supremely accurate doing math calculations by hand may be behind us. Every smartphone in the world possesses the capacity to instantly solve the most complex equations correctly. We can easily activate our voice recognition software to carry out calculations for us in mere seconds. However, so far, computers cannot solve complex real-world problems. Humans must still define the problems that need to be solved and the calculations required to solve them, and they must interpret the answers in relation to the original question. So far, only humans are fully capable of applying mathematics to understand, define, design, and build the world around us.  

With the end goal of nurturing and empowering the problem-solvers of our future, how do the educator heroes in our nation’s classrooms help their students develop the flexibility and ingenuity to apply and transfer mathematical skill and conceptual understanding in order to solve complex tasks? That sounds like a rich and important conversation, and it is one I am eager to have!