Written By: Danielle Descarfino, Fifth Grade Teacher at P.S. 94 in Brooklyn

Getting Started

From the beginning of the school year, I used Exemplars problem-solving tasks regularly to create routines that have helped my fifth grade students grow and succeed. Following the Problem-Solving Process is a central part of this.

Although each task is different, the procedure helps kids internalize a framework for approaching a problem. I provided each student with his or her own color copy (in a sheet protector for safe keeping.) Each time we begin an Exemplars task, the students take out their Problem-Solving Procedures and refer to it. I also have a poster-sized version prominently displayed in the classroom, which I hold up and point to while guiding and facilitating tasks.

Building Background Knowledge

My class is made up of English Language Learners and former English Language Learners, so I anticipate that reading and understanding the problem may be especially challenging for them. We read the problem together, I ask questions to activate their background knowledge, and I often provide pictures that help them visualize the problem.

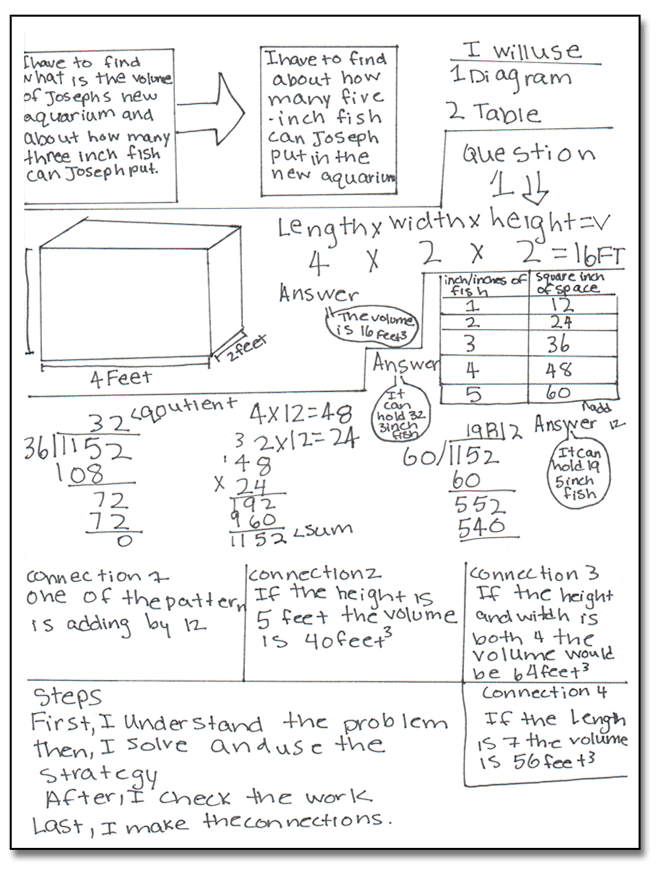
For example, we recently completed “A New Aquarium,” a 5.MD.C.5a task involving volume. We had been working on this math concept for only a few days and this was our first volume Exemplars task. Before reading the problem, I displayed a photo of an aquarium on the Smart Board and discussed the following questions with the class:

• What is an aquarium?
• What type of solid is this aquarium?
• How could you figure out how much space this aquarium takes up? What steps would you take?

Although many students initially were not familiar with the word “aquarium,” after this discussion, they understood that an aquarium is a fish tank and a rectangular prism, which meant that we would be calculating its volume to find out how much space it takes up. Using visual aids and background questions to ensure that students understand the situation in the problem has been very helpful when completing Exemplars with English Language Learners.

Differentiation

We always utilize the differentiated Exemplars tasks. Students are aware of which problem-solving group they are in and know where to sit when it is time for an Exemplars task. One group gets the More Accessible Version; they are guided through the problem as they work with the Special Education teacher at a kidney-shaped table. The other two groups receive the Grade Level and More Challenging versions and sit with their groups in desk clusters, like a team of problem solvers.

For the Grade Level and More Challenging groups, we discuss background information, read the problem out loud, annotate it, and write our “I have to find …” statements. Then the students go on to work with their groups to complete the task while the teacher takes on the role of a facilitator, conferring with groups. Students share ideas, address misconceptions, and explain their mathematical reasoning to one another as they solve.

Motivating Students

I love hanging Exemplars tasks on bulletin boards. I think it’s useful for students to look at the page and see all of the different ways their classmates organize and express their mathematical thinking through equations, representations, and writing.

From day one, I have made it clear that it is expected that their finished work clearly communicate their problem-solving steps to the reader. Not only should the students make an effort to write neatly, but they should also organize their problem-solving steps on the page in a way that makes sense. Sometimes if a student is not showing all of their steps or it is unclear, I’ll say, “I am confused. When I look at your paper, I don’t understand the steps you took to solve the problem.” When the students have the understanding that a goal is to communicate their math thinking to a reader, it helps them create a higher-quality finished product.

Another great way to motivate students is through mathematical connections. I have given a strong emphasis to connections, as I initially noticed that once students solve the problem, they feel like they are done! This is not the case, because noticing mathematical connections, patterns, and alternate strategies really helps students understand mathematics on a deeper level and practice critical thinking skills.

To help them stretch their thinking, I discourage students from writing “boring” connections, like “This number is greater than that number” or “John ate the least amount of pizza.” Instead, I encourage them to use mathematical language, create a second representation, show steps to solving with alternate strategies, convert fractions/decimals/percents, or extend the problem by adding to the story in the original problem. Once they get the hang of it, they start being more creative, going above and beyond to make more complex math connections. During the volume unit, I taught students how to use grid paper to make scaled models of rectangular prisms. When completing these tasks, many students decided to build models to represent the rectangular prisms in the task and attach them to make 3-D Exemplars. They looked great, and the students loved making them!

Peer Assessing

At the beginning of the year, I explained each portion of the Exemplars rubric to the students. The rubrics are very student-friendly and I find that they inspire students to want to become Experts.

Each time I assess Exemplars, I use the rubric along with a sticky note full of feedback. The sticky note always contains one “Glow,” something the student did well, and one “Grow,” something the student could improve upon. At the beginning of the year, I let the students know that when they become more comfortable with Exemplars, they would learn how to peer assess. After a few months, I told the students that they were ready to peer assess one another’s work. They were so excited! This made them feel proud that they had reached a new level of expertise in problem solving and feel empowered that they were now trusted to assess a classmate’s work.

To peer assess, they do exactly as the teacher has done all year: complete the student rubric and use a sticky note to write “Glow and Grow” feedback. An example of this can be seen below. From the start, I was so impressed at how well the students were able to assess one another’s work with Exemplars. I found that regularly providing students with written feedback and referring to the rubric when expressing expectations is a great way to model peer-assessment. Furthermore, the experience of assessing Exemplars helps students get new ideas from their classmates and become more aware of how their own work will be graded.

Task: A New Aquarium

(More Accessible Version)

Joseph has a new rectangular aquarium. The aquarium has a length of four feet, a width of two feet, and a height of two feet. What is the volume of Joseph’s new aquarium? An aquarium holds one inch in length of fish for each twelve square inches of the area of the base of the aquarium. Joseph can buy fish in two different sizes—about three inches in length or about five inches in length. About how many three-inch fish can Joseph put in the new aquarium? About how many five-inch fish can Joseph put in the new aquarium? Show all your mathematical thinking. 

View Grow and Glow

Danielle’s Biography

Danielle Descarfino is a fifth grade teacher at P.S. 94 in Sunset Park, Brooklyn. She graduated from Fordham University with a Masters of Science in Teaching English to Speakers of Other Languages. Danielle grew up in Tappan, New York, and currently lives in Brooklyn. She was inspired to become a teacher after spending time as a volunteer teaching English at an orphanage and community center in Salvador, Brazil.