Written By: Dinah Chancellor, Exemplars Math Consultant

Prior to 2006, many states—including Texas—had a math curriculum that was perceived to be “an inch deep and a mile wide.” Teachers were required to teach a large number of math skills that spiraled from grade to grade and seemed both disconnected and fragmented. When Texas’ own Cathy Seeley became President of the National Council of Teachers of Mathematics (NCTM), she determined that a more focused mathematics curriculum that was built around fewer “big ideas” would give students and teachers the luxury of time—time to plumb the depths of major math concepts, and time to form a foundation of connected mathematical understandings.

Therefore, in 2006 NCTM published the Curriculum Focal Points—A Quest for Coherence. The Texas response to the Curriculum Focal Points was the new state assessment program—STAAR—the State of Texas Assessment of Academic Readiness taken by students in grades 3-8. STAAR focuses on fewer skills at each grade level and it is expected that these skills will be taught at greater depth. When the new math TEKS were written, released in April 2012 and implemented in the fall of 2014, the writing teams focused on fewer skills at each grade level. Teachers are expected to address these skills and understandings by teaching rich lessons in which students make critical connections between foundational big ideas in mathematics. Because of the need to teach a focused mathematics curriculum, it does not make sense to teach each of the new math TEKS in isolation.

Problem Solving for the TEKS

To assist Texas educators in achieving this goal, Exemplars latest K–5 product, Problem Solving for the TEKS, groups the individual math TEKS student expectations into rich Units of Study. Four or more instructional tasks/formative assessments and one or more summative assessment is provided to address the big mathematical ideas within each Unit. Tasks are meant to supplement a school or district’s existing curriculum. Teachers may choose to use all or only a few of the instructional tasks/formative assessments in a Unit. The summative assessments include anchor papers that exemplify each of the performance levels in the Exemplars Rubric—Novice, Apprentice, Practitioner (meets the standard) and Expert.

A Look at a Sample Unit

The Place Value Unit represents one of eleven Units in the third grade. The math TEKS covered in this Unit include: 3.2A, 3.2B, 3.2C, 3.2D. These math TEKS were grouped together to provide a cohesive Unit that enables 3rd grade students to understand the Properties of Place Value and to apply this understanding to compare and order whole numbers. See the full list of Units of Study for K–5.

How Might a Teacher Use the Tasks in This Unit?

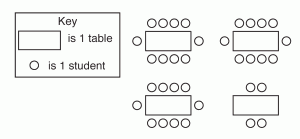
As the Place Value Unit progresses, a teacher may want to use one of the instructional tasks to teach students the expectations of the Exemplars Assessment Rubric. A lesson using the task “Tables for a Party” may include the following steps:

•  Whole Group: Read the task together and ask students to underline the question, identify important information in the problem and summarize the task by restating what the question is asking them to do. Example: I need to find out how many tables need to be set up for 34 students with no more than 10 students sitting at each table. On the Exemplars Rubric, this step is scored in the category for Problem Solving—Does the student understand the problem?

•  Small Group: Ask students to work together, think of a plan, and write it down. Example: I will draw a diagram of tables with students sitting at them. At this point, students will implement their plan to solve the problem.

Example:

(Refer to the task Planning Sheet for additional examples of solution strategies.)

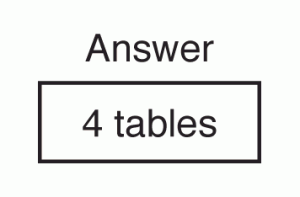
 Students will check their plan to make sure it works and put a box around their answer.

Example:

On the Exemplars Rubric, this step is scored in the category for Problem Solving—Does the student have a plan? Does the student get the correct answer? It is also scored in the category for Reasoning and Proof—Does the student show a systematic implementation of the plan?

Small Group: Ask students to polish their papers—

• Organize your solution.
• Explain your plan and how it solved the problem.
• Create a representation—such as a diagram with a key, use a model (such as manipulatives), use a table, use a number line.
• Use mathematical vocabulary and/or symbolic representation.
• Label your solution.
• Show your answer. Put a box around it. Make sure it answers the question.

On the Exemplars Rubric this step is scored in the category for Communication—Does the student use at least two mathematical vocabulary words, at least two correct symbolic representations or one of each? It is also scored in the category for Representation—Is the representation correct and appropriate to the solution?

 Small Group: Finally, make a connection—

• Make an observation.
• Identify and describe a pattern.
• Make a comparison between this task and other tasks. Explain how the math is similar.
• Identify a rule.
• Create a hypothesis or conjecture to test.
• Solve the problem using a different strategy to prove the original solution is correct.
• Recreate the problem and show a different solution.

On the Exemplars Rubric, this step is scored in category for Connections—Does the student include a mathematically relevant connection? Making connections requires students to look at their solutions and reflect.

Using Anchor Papers & Scoring Rationales

Anchor papers and assessment rationales are provided with every summative assessment task. These problem-solving tasks are given at the end of a Unit of Study to assess students’ understanding. A summative assessment must represent a student’s total independent solution. One Hundred Miles is the summative assessment for the grade 3 Place Value Unit.

Anchor papers and scoring rationales provide a great way to show both teachers (in professional development sessions) and students the expectations of the Exemplars Rubric; i.e. What a Practitioner (meets the standard) piece of student work looks like. Analyzing Exemplars anchor paper solutions and rationales at the Practitioner and Expert levels help students polish their own work and measure their own progress toward a specific goal. Analyzing the Novice and Apprentice samples can help identify for students where the work falls short of the goal and specifically how the papers could improve.

To view other sample tasks and anchor papers for grades K–5, you can sign up for a free 30-day Trial for Problem Solving for the TEKS.