On-Demand Webinar Focus: Grades K-2

On-Demand Webinar Focus: Grades 3-5

At the heart of Exemplars, our goal is to help develop strong problem solvers for the 21st century. Research has provided evidence that effective problem-solving skills can be developed through regular practice with the fundamentals of the problem-solving process. Application of these skills instill the mindset that any problem can be solved.

Exemplars created a problem-solving process built on the timeless work of George Polya, who researched the processes of great thinkers and distilled their methods into 4 specific steps.

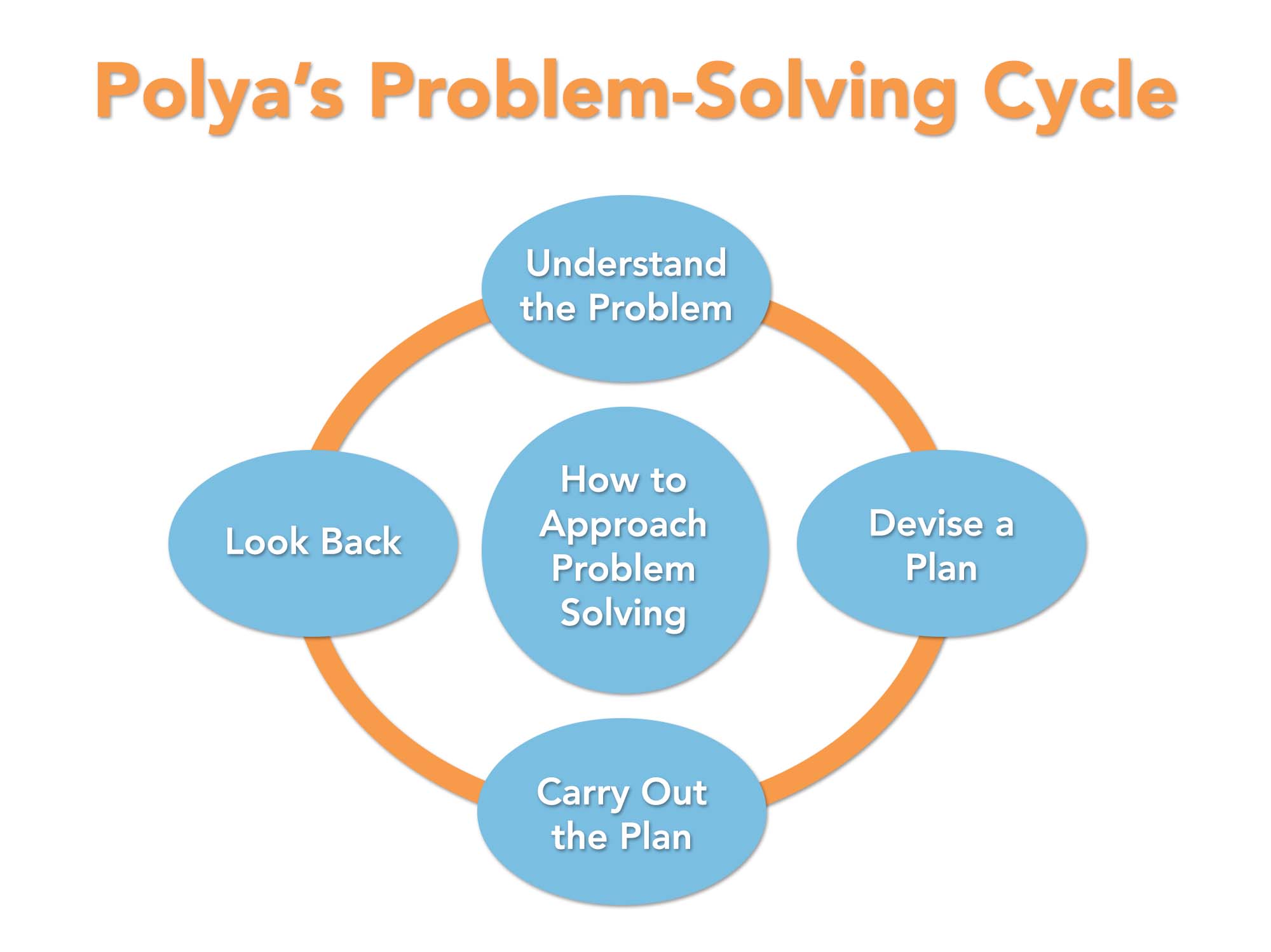
Exemplars took this work and created its Problem-Solving Procedure, which includes specific ideas that add detail to each stage. Our Problem-Solving Procedure asks students to:

1. Understand the problem they need to solve and distill it down into their own words.
2. Think of a plan they can use to solve the problem. This plan includes a strategy or representation they think will help them reach a solution.
3. Solve the problem using their strategy.
4. Provide a solution that shows their mathematical thinking, including: 
   • a representation of their conceptual thinking,
   • an explanation of their mathematical reasoning, and
   • written communication of their strategy as well as appropriate math vocabulary.
5. Define connections between the task and other mathematics, including finding patterns, solving the problem another way, defining a rule, etc.

A “written” solution is considered fundamental at Exemplars. As part of this process, we ask students to think deeply about the NCTM Mathematical Process Standards and Common Core Mathematical Practices. Exemplars has spelled out these expectations in its rubric, which uses the same criteria and 4 levels of performance from Kindergarten to 12th Grade.

Exemplars Standards-Based Rubric

Second Grade Student Solution - Sample

When using the full suite of Exemplars materials (problem-solving performance tasks, Preliminary Planning Sheets, Problem-Solving Procedure, and scored student anchor papers), teachers and students can grow into strong problem solvers who understand the value of evidence-based arguments.

What aspect of mathematics are we going to concentrate on in the 21st century? With time for intentional application, our students can become the great problem solvers we need them to be.