Bridge the Gap Between Common Core, Your Classroom and the Real World

Written By: Elaine Watson, Ed.D., Exemplars Math Consultant
To most nonscientists, mathematics is counting and calculating with numbers. That is not at all what a scientist means by the word. To a scientist, counting and calculating are part of arithmetic and arithmetic is just one very, very small part of mathematics. Mathematics, the scientist says, is about order, about patterns and structure, and about logical relationships.
Keith Devlin, Life by the Numbers
The word “scientist” above could be replaced by the word “doctor, lawyer, engineer, accountant, CEO, military officer, government worker, homeowner, citizen …” In other words, anyone who uses numbers to make decisions needs to look beyond the calculations and be able to discern what the numbers are telling them.
Math textbooks have developed “word problems” in response to the question so often asked by students as they learn to follow algorithms and solve equations in order to find the correct answer: “When am I ever going to use this in real life?” The question is often answered by the jaded teacher, who has heard it from each new generation of students in this way: “You’re going to use it on the test!” This answer seals the students’ belief that what they learn in math class is not applicable to the real world, but merely a set of exercises that need to be done in order to pass the course.
Past mathematics standards documents have focused on the hard content, the factual and procedural content students should learn, which is of course important. The focus on the soft content, the habits of mind and thought processes that are practiced by students when solving a problem, has traditionally either been relegated to the end of the standards document as an afterthought or omitted altogether.
The Common Core State Standards in Mathematics (CCSSM) recognize that the soft content, the practices students used to approach and solve a mathematical task, are as important as the hard standards. Soft does not mean unimportant. In the same way that a computer (hardware) cannot function effectively without appropriate software, CCSSM Content Standards cannot be accessed and used without students using the supporting Practice Standards.
The Practice Standards have to be learned, and practiced, alongside the Content Standards, but because of the “soft” nature of Practice Standards, they are harder to pin down. Phil Daro, one of the three authors of the CCSSM, describes the Practice Standards as “the content of a student’s mathematical character.”
It is important to remember that it is the students who practice the Practice Standards. Teachers should model the practices in their instruction, but more importantly, teachers should explicitly plan lessons that include teacher pedagogical moves, student activities and tasks that will elicit the Practice Standards in students.
The tasks created by Exemplars are excellent examples of rich problem-solving that naturally elicit the Practice Standards. Below we will look at the Grade 2 task “Barnyard Buddies” and discuss how it meets each of the eight Mathematical Practice Standards as well as content standard 2.OA.A.1.
Barnyard Buddies
A farmer has 8 cows and 10 chickens. The farmer counts all the cow and chicken legs. How many legs are there altogether? Show all your mathematical thinking.
CCSSMP.1 Make sense of problems and persevere in solving them.
There is no hint in this task as to how to go about solving the task. It is not a generic type of problem with which the student has had previous experience. The student must make sense of the task before being able to develop an approach for solving it. Some approaches may be more efficient than other approaches.
CCSSMP.2 Reason abstractly and quantitatively.
In order to solve the problem, students will need to use an approach in order to organize their thinking and keep track of the quantities involved. One approach is to draw 4-legged animals and 2-legged animals and count. Another approach is to create a table. Both of these approaches have created an abstraction (mathematical model) of the situation. The student work below shows how two students modeled the problem.
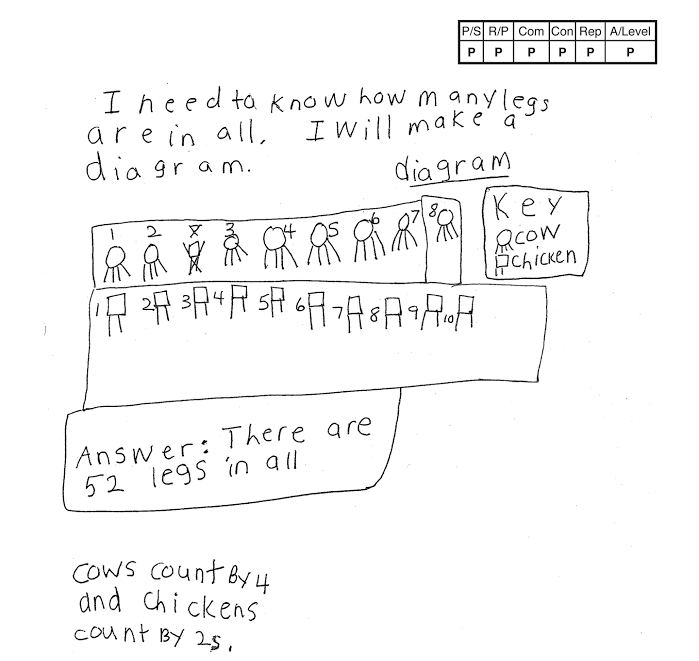
Student 1 created abstractions of the chickens (square with 2 legs) and cows (circles with 4 legs).
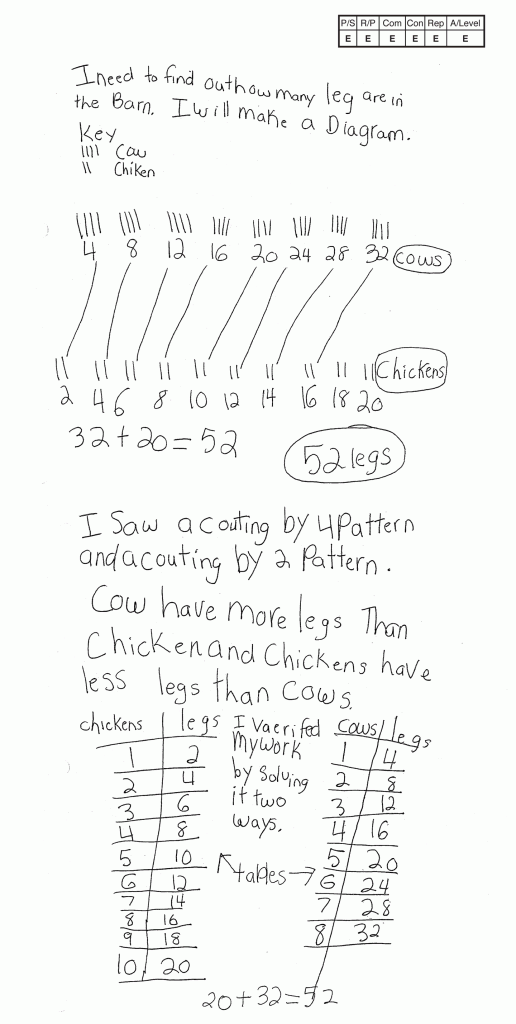
Student 2 simply drew the legs without the bodies, which was a step toward greater abstraction. She or he then went on to use an even more abstract approach by noticing that there was a pattern and deciding to use a table. This student work is also a good illustration of Practice Standard 8: Look for and express regularity in repeated reasoning.
CCSSMP.3 Construct viable arguments and critique the reasoning of others.
This task will elicit a lot of different ideas as to how to approach it. Students will need to persuade others as to why their approach will work the best. In order for students to exhibit this practice standard, a classroom culture needs to be developed where student discussion of their work is the norm. The teacher’s role is to encourage the discussion and question and guide as needed.
CCSSMP.4 Model with mathematics.
In order to solve this task, students will need to go through the steps of the Modeling Cycle. They formulate an approach, compute, and then check their answer to see if they have correctly counted all 8 cow’s legs and all 10 chicken’s legs. If their answer makes sense, they report it out. If it doesn’t make sense, they need to go back through the cycle, determining where they went wrong. Were their pictures correct? Did they have the right number of each type of animal and the correct number of legs on each type of animal? If they used a table, did they skip count correctly by 2 and by 4? Did they add correctly? The cycle continues until they are satisfied that their result is a viable answer for the problem.
CCSSMP.5 Use appropriate tools strategically.
Tools are not necessarily physical, like a ruler or a calculator. On this problem, the student’s drawing or table can be considered a tool, since it helps make sense of and solve the problem.
CCSSMP.6 Attend to precision.
Precision is needed in the drawings or table, in the counting, and in the addition. Students also need to be precise in labeling their answer. If a student answers with only a number without the label “legs,” they are not attending to precision.
CCSSMP.7 Look for and make use of structure.
The student needs to visualize the structure of the situation. In this case the structure involves a given number of animals with 4 legs and a given number of animals with 2 legs. That structure will inform how the student approaches and solves the problem. If the student notices that 4 consists of 2 copies of 2, this will help in counting, since he or she should be proficient at counting by 2s.
CCSSMP.8 Look for and express regularity in repeated reasoning.
The student is repeatedly adding 2 or adding 4 for a given number of times. The student can count by 2s while pointing to each chicken. For the cows, students can either count by 4s, or they can count by 2s when pointing to the cows and touching each of the two pairs of legs on every cow.
Support for Common Core Content Standards
In addition to eliciting the Common Core Practice Standards, Exemplars tasks are also aligned Common Core Standards for Mathematical Content.
To solve “Barnyard Buddies,” students need to model the situation by using some type of drawing to represent the 10 chickens and the 8 cows as well as the number of legs on each animal. Creating such a representation is an early form of algebraic thinking. After developing the pictorial model, students then need to count the total number of legs. Most students will skip count by either 2 or 4. Some students may organize their counting by making groups of 10 (2 cows and 1 chicken or 5 chickens). Whichever approach students use for counting, they are recognizing a numerical pattern, which is also an underpinning of algebraic thinking. This type of thought process is best matched by the Common Core Domain Operations and Algebraic Thinking. Within this Domain, “Barnyard Buddies” aligns with the cluster, Represent and solve problems involving addition and subtraction. The specific content standard addressed is 2.OA.1.
2.OA.1 Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.